Using a Genetic Algorithm for Hyperparameter Selection

This is a blog post credit to Joseph Como, Rohan Mirchandani, Max Popken, Netra Ravishankar

Motivation for the Algorithm:

Hyperparameter optimization is an important part of creating an accurate machine learning model. Model hyperparameters are values that dictate the structure of the model, and thus contain information about the model itself, not necessarily the training data fed into the model. Optimizing the hyperparameter set allows for more accurate learning of state-specific parameters (such as nodes/weights) that are computed when training the model on the data.

Two existing forms of hyperparameter optimization used in practice are grid search and randomized search. Grid search is the most commonly-used method in practice. It involves brute-force searching every possible combination over a set over hyperparameter ranges. It creates a model with each set of hyperparameters, evaluates its accuracy, and returns the set of hyperparameters that produce the best model. While grid search is typically exhaustive, it is very computationally intensive and grows exponentially with the number of hyperparameters and corresponding range sizes. As a result, only very small regions of the hyperparameter space can be explored, so often the optimal solution is not found. Randomized search operates similar to grid search, but instead of taking all combinations of hyperparameters over given ranges, it tests combinations randomly and chooses the best one. Randomized search has been shown to produce similar results to grid search while being much more time-efficient, but a randomized combination approach always has a capability to miss the optimal hyper parameter set. While grid search and randomised search are decent ways to select the best model hyperparameters, they are still fairly elementary.

We will explore a more sophisticated method of parameter optimization known as "evolutionary optimization", which follows a process based on Charles Darwin's theory of natural selection. In natural selection, a population consists of individuals, each containing a set of genes that can be either beneficial or detrimental to the individual's probability of survival. An individual's fitness is a measure of how beneficial on aggregate their genes are to their survival, so the fittest individuals will survive while the least fit individuals will not. This phenomenon is called survival of the fittest. Since only the individuals that survive can reproduce, only the beneficial genes will be passed on to the next generation. This means that later generations will have genes more conducive to survival, and the individuals on average will be more fit. After we apply this process for several generations, we are left with a population which has selected for only the most beneficial genes.

The specific evolutionary optimization algorithm we are implementing is a variation of the "Genetic Algorithm". We treat each of the points in the hyperparameter space as an individual. These points consist of values for each of the hyperparameters being considered, which are analogous to the genes in each individual. We can randomly select a certain number of points from our hyperparameter space, which will be our initial population. For each generation, or iteration of the algorithm, we simulate mating and random mutation by generating new points from the existing population. Then, only the "fittest" points who produce the most accurate models will survive and become the starting population for the next iteration. The goal is that just like natural selection results in populations with higher fitness, our algorithm will result in a final population of points in our hyperparameter space that are optimised to train models.

The following high-level pseudocode of our genetic algorithm illustrates this process:

1. Generate initial population from parameter ranges
2. Apply matching and crossover functions to the population to create offspring; add offspring to the population.
3. Apply random mutation function on offspring to create mutants; add mutants to the population.
4. For each individual in the population, train a model with that individual's set of hyperparameters and obtain "fitness" score (model accuracy).
5. Sort individuals by score and set new population to be the fittest individuals.
6. Repeat steps 2-5 until a preset stopping condition is met (either number of iterations or sufficient model score), fittest individual is optimal set of hyperparameters.

Description of the Main Subroutines:

The genetic algorithm for hyper parameter tuning involves three fundamental sub-routines: the matching function, the crossover function, and the mutation function.

The purpose of the matching function is to select who among the population is paired with whom. Its biological analogue is the process by which individuals in a species select whom to breed with. Typical individuals will favour fitter mates as this will lead to stronger offspring who have a greater opportunity to survive, reproduce, and propagate their genetic information throughout the population. Our current implementation mimics this by assigning each member of the population a certain fitness. Since the objective of these models is to get the lowest possible generalisation error, and we seek to optimise this by minimising the error on a training set, we assigned each member of the population a fitness score that was a function of its training error. Lower errors correspond to lower models, so the exact fitness was the reciprocal of this error. Each member is then assigned a selection probability proportional to its fitness score – precisely, each member's probability of selection is its score divided by the total score of all the members. A number of members equal to the original size of the population was then drawn based on this probability distribution, with subsequent selections paired for "breeding". This approach stuck to the biological principle that individuals tend to prefer fit mates because the individuals with the highest fitness had the highest probability of selection; however, it is still rather crude and has some potential improvement to be discussed later.

The next step in the genetic algorithm is the crossover function. This is the process by which a child is generated from its two parents, and is built to model the biological process of sexual reproduction. During sexual reproduction, a child is generated by sampling some of the genes from both its mother and father. This is to ensure that the child contains genetic information from both its parents so that this genetic information is able to spread through the population. However, it also ensures that the child is unique from both of its parents, which is important to maintain genetic diversity within the population – in the context of hyper parameter selection, this allows us to sample more of the hyper parameter space rather than simply resampling the original values. There are several approaches to this, each with its own biological justifications, but the one we chose to implement was random crossover. In this approach, each gene for the child is sampled independently from both parents' corresponding genes. For example, if this algorithm were implemented for Random Forest with the number of estimators being one of the hyper parameters, then the child's number of estimators would have a 0.5 probability of being either that of its first parent, or its second parent. Using this approach, each of the pairs decided by the matching function produced two offspring, each of whose hyper parameters are selected in this way. This follows the biological model because each offspring has a piece of its genetic information from both of its parents – its values are sampled directly from theirs. However, it also ensures its diversity, because except for in the very rare case where the child samples all of its hyper parameters from the same parent it does not copy an entire parent "genome". Therefore, by using this crossover approach, we are able to preserve the hyper parameters of the parents (which we know from the matching function represent the stronger members of the population) while also introducing diversity.

The final sub-routine of the genetic algorithm is the mutation function. Within a species, mutations are the key way in which novel genetic material is introduced, which is ultimately what allows it to evolve. These mutations can be either positive or negative, but by keeping the positive ones and eliminating the negative ones through natural selection, over generations the species can develop traits conducive to its survival. Our algorithm seeks to emulate this. Typically in biology, these mutations are introduced during reproduction while the child's genes are sampled from the parents. Therefore, our current implementation introduces these mutations immediately after the crossover function generates the offspring from the parents. At this point, we use a predetermined mutation rate to determine which hyper parameters are to be mutated. Each hyper parameter is selected independently with a probability equal to the mutation rate, and the selected hyper parameters are set to a random value within the allowable range. The purpose of the mutation function is exactly as in its biological analogue: to introduce new, potentially beneficial traits to the population. This allows the algorithm to search regions of the hyperparameter space which were not represented in the original population, but which may contain a better hyper parameter selection. This approach allows the algorithm to "evolve" to better hyper parameters, with the end goal of arriving at the global minimum hyper parameter vector.

Different Strategies for Crossover, Matching, and Mutation :

Matching:

There are several different methods for implementing crossover, matching, and mutation. The purpose of the matching function is to pair individuals together for breeding in a manner that prioritizes individuals with the best parameters to ensure that these parameters are passed on to the next generation. In our genetic algorithm, we only look at the fitness of each individual, also known as the mean absolute percentage error. However, this often leads to too much homogeneity because it involves matching two very similar individuals that could be related to each other as a parent, child, or mutant, or matching an individual to itself. This form of inbreeding is detrimental to the population because it removes diversity from our population and it steers the algorithm towards a local minimum and away from finding an optimal solution. In order to reduce homogeneity in our population, we will implement two different matching methods. In the first method, we will group individuals with similar fitness scores together. For each individual, we will add up the values of all the parameters, except the fitness score, and compare this sum to every individual in the group. Then, we will match individuals with greater differences in their sums together. By matching individuals in this manner, we reduce the risk of matching related individuals with each other or matching individuals with themselves. This introduces diversity into our population and allows us to pass on a larger variety of parameters that results in high fitness scores to the next generation.

Another matching method we will implement to preserve diversity in our algorithm is to run multiple populations simultaneously, independent of one another. Towards the end, we will introduce all the populations together and run a few more generations to determine the model. This method would help eliminate convergence to a local minimum because the probability that two or more populations converge to the same local minimum is very low, meaning when all the populations are reintroduced, there will be more diversity than if we ran a single population. Additionally, since we will have several local minimums, we will be able to take the best parameter values from these minimums to better estimate the global minimum, or we can cross all the local minimums together to arrive at a new minima. This method mirrors natural selection, where multiple populations evolve in geographic isolation and develop different traits in their respective environments.

Crossover

Next, we will adapt the crossover function. The goal of the crossover function is to organize our population into pairs and take genes from each individual in a pair and combine them to create a new individual, also known as the child. Currently, the crossover method we implemented looks at each parameter in a pair, randomly selects a copy of this parameter from an individual in the pair, and passes it down to the child individual. In order to optimize our algorithm, we will explore different variations of this random crossover method. In the first variation we will attempt to mimic the crossing over pattern that chromosomes undergo during meiosis and mitosis. Instead of looking at each gene, we will make a random number of partitions and take alternate sections from both of the parents at these partitions and pass them onto the child. For each partition, we will generate a random number between 1 and which will represent the index of the parameter at which we will place the partition. For instance, if we had two parent individuals with genes each and we generated 3 partitions at the parameter indices 2, 3, and , the child individual would be created in the following manner.

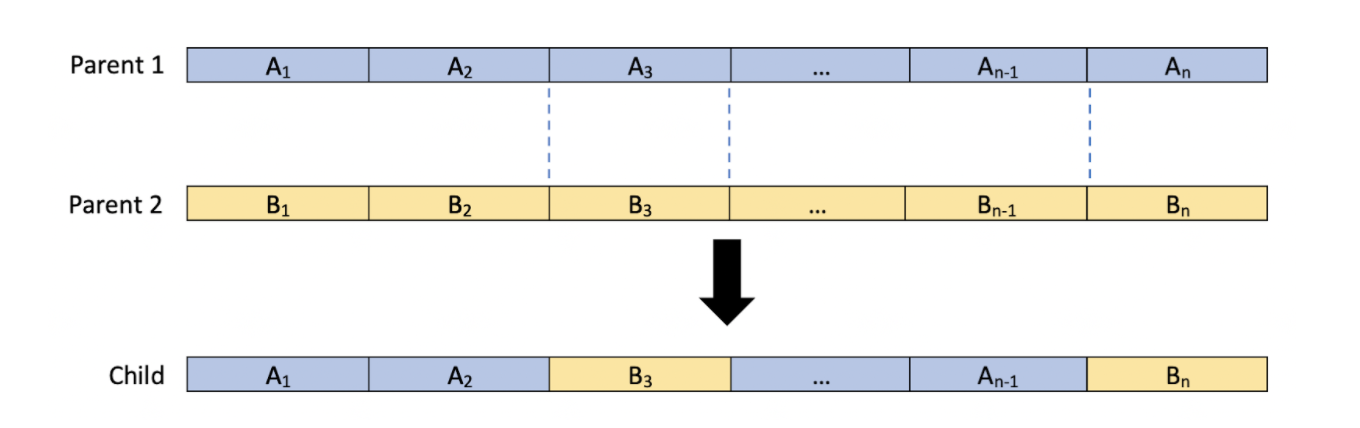
This method performs random selection on sections of the parameters instead of each individual parameter itself, which allows for groups of parameters to be passed on to the next generation.

Another method we will explore is random crossover at randomly picked genes. Similar to our current implementation, this method will choose which parent will pass down a certain parameter with probability 0.5. However, instead of performing this randomization on each parameter, we will randomly select a certain number of parameter indices and conduct the randomization on these parameters. The remaining parameters will be passed down from the first parent. The diagram below shows the case where we have two parent individuals with genes each and we choose to randomize on genes 1, 3, and .

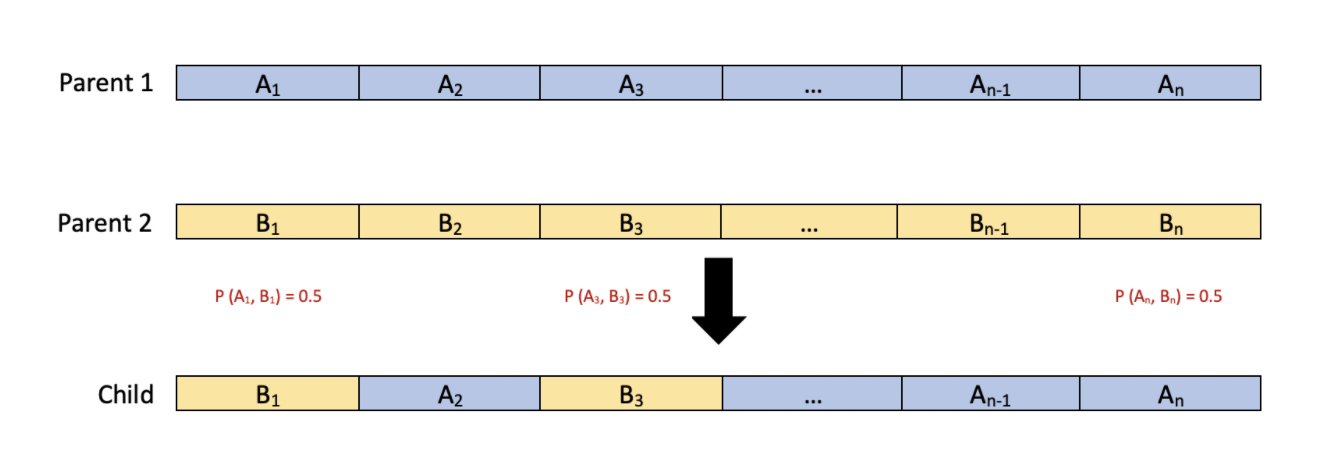
The method above can also be repeated by choosing the remaining parameters from Parent 2 instead. Since the number of parameters we choose to randomize and the location of the parameters we choose to randomize are chosen at random for each pair of parents in the population, this method of crossover promotes diversity among the children and it looks at different groupings of parameters in an individual.

Another possible strategy for creating children would break from the conventional idea of "crossing". As we know in biology, when two parents mate, the child tends to have features that are a mix of the two parents'. Thus, there are many different strategies we can enforce that could diversify the child. Given parents

We could have enforce the algorithm to create children in any of these ways:

In the first row, we see that each feature of the child is simply the average of the features of the two parents. The second row simply chooses a value uniformly between the two parents. Both of these strategies yield a child that has features that are between the features of its parents. The benefit of such a strategy is to find some sort of middle value between the two parents that is more optimal than both of the values that the parents have. This strategy is successful if the true optimal value lies between the parents' values. However, where such a strategy could go wrong is that it could create a more homogeneous population. There is a probability of 0 that a child could have a value that does not lie between the values of its parents' features. This could create a homogeneous population if we see the features in each generation converge to similar values.

Mutation Alternatives:

A crucial element in any genetic algorithm is the mutation phase. As a species evolves, new members are born with mutations. These mutations can be advantageous, disadvantageous, or vestigial. As species evolve, the specimens with the advantageous mutations procreate to introduce more specimens with the advantageous traits into the population. In the context of our genetic algorithm, we introduce a random mutation in order to emulate the above process with the hope that one of these mutations will be advantageous and thus this child/mutant will survive. In our current implementation, our mutation function looks at each individual's features and with probability p, mutates it. Once a feature is chosen to be mutated, it is replaced with a random value that is chosen from a uniform distribution U[a,b], where the values a and b are chosen to represent realistic boundaries that a feature could take on. Example. We can have:

Where k and j are the lower and upper boundaries respectively of realistic values. The benefit of such a method is to possibly escape a situation where one feature is negatively affecting the score of a member of the population. A downside, however, is that good features can be eradicated.

Another potential strategy for mutation would be to perturb a value of one of our features randomly. Each feature would still have the same probability of being mutated, however, now U[k,j]we could mutate the desired feature like so:

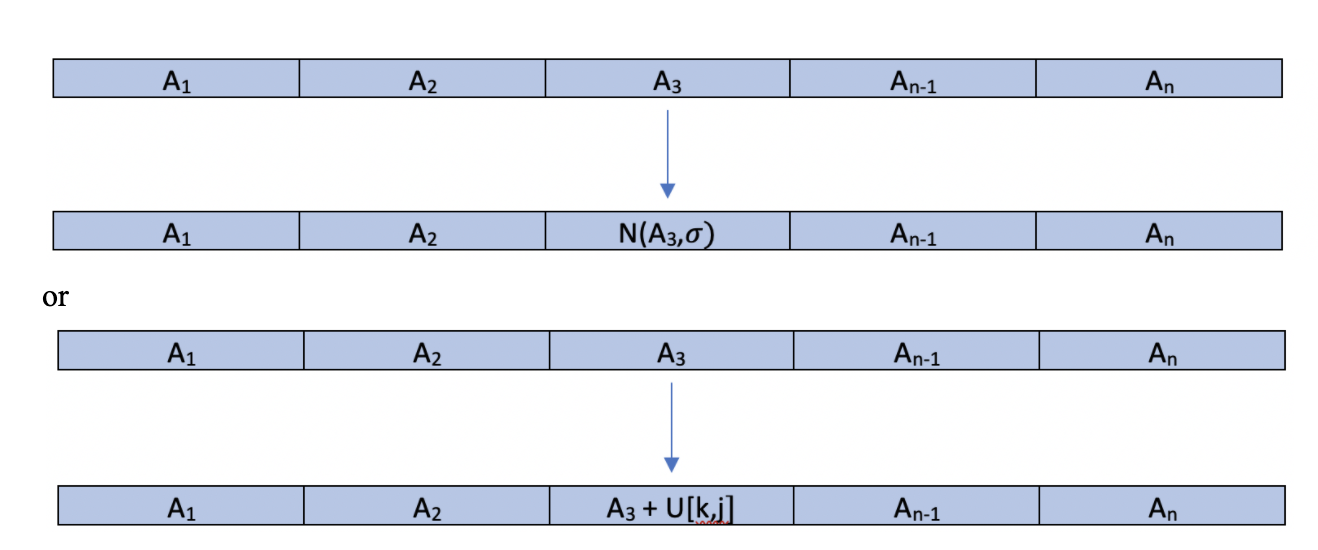
Note that these methods offer mutations of variables that are based off of the original feature value. The benefit of such a strategy is that we could be taking a good feature and slightly tweaking it to make it better. However, the downfall of such a method is tweaking a poor feature and making no material change. Furthermore, we want to avoid creating a homogeneous population. The benefit of large, random mutations is that it allows the algorithm to search a larger portion of our parameter space.

When we further explore our genetic algorithm, we will look to find ways to both search a large portion of our parameter space but also narrow in on better solutions in specific areas of the parameter space. One way to do so is to encourage many mutations in earlier generations of our population. As more of the parameter space has been explored, we can narrow in on areas of our parameter space that seem promising, and limit mutations and crossovers that promote growth in these areas.